Posiciones de dos rectas
Dos rectas en el plano
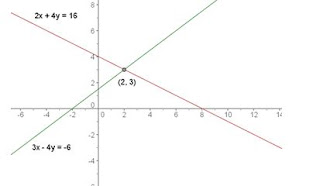
Secantes
Dos rectas son secantes si
sólo tienen un punto en común.
Son las rectas que se cruzan
en un punto
Dos rectas son coincidentes si tienen todos los puntos son comunes.
Dos rectas son coincidentes si tienen todos los puntos son comunes.
Rectas definidas por un punto y un vector
Rectas definidas por un punto y un vector


Dos rectas son coincidentes si tienen todos los puntos son comunes.
Dos rectas son coincidentes si tienen todos los puntos son comunes.
Rectas definidas por un punto y un vector
Rectas definidas por un punto y un vector
Posición
|
r
|
r'
|
Cruzadas
|
3
|
4
|
Secantes
|
3
|
3
|
Paralelos
|
2
|
3
|
Coincidentes
|
2
|
2
|


Paralelas
Dos rectas son paralelas si
no tienen ningún punto en común.
El sistema de ecuaciones
formado por las dos rectas no tiene solución.
Coincidentes
El sistema de ecuaciones
formado por las dos rectas tiene infinitas soluciones.
El sistema de ecuaciones
formado por las dos rectas tiene infinitas soluciones.
= rango de la matriz
ampliada.
Las posiciones
relativas de dos rectas vienen dada por la siguiente tabla:
Ejemplos
En primer lugar se pasan las ecuaciones continuas a ecuaciones implícitas.
En primer lugar se pasan las ecuaciones continuas a ecuaciones implícitas.
Determinamos
el rango de la matriz ampliada.














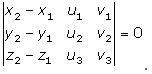






No hay comentarios:
Publicar un comentario